▷ Fractales ¡Significado, origen y TODA la información!

¿Porque vemos la misma estructura repetida por doquier en la naturaleza? para responder a estas preguntas tenemos que recurrir a unos objetos geométricos que son a la vez extraños y omnipresentes, mejor conocido como los fractales.

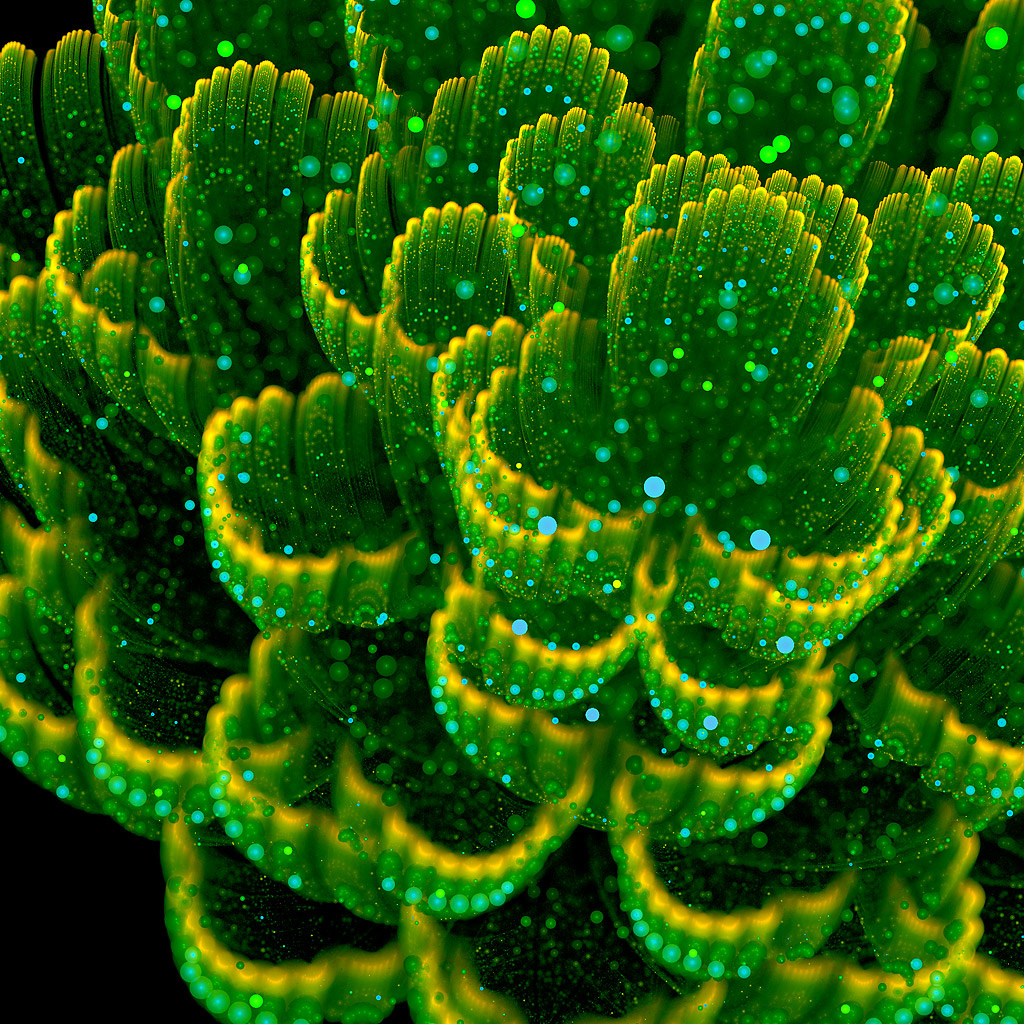
Un fractal es un objeto geométrico cuya configuración aparentemente al azar, se repite a diferentes escalas. pueden ser creados a partir de procesos matemáticos o se pueden presentar como fractales de la naturaleza.

La auto similitud se aplica a todas las escalas de detalle, lo cual implica que el universo tiene detalles infinitamente pequeños. Aunque escojamos una parte muy pequeña, esa parte es igual de compleja que el todo fractal.

Este término fue propuesto por el matemático Benoît Mandelbrot en 1975, quien nos explica que muchas estructuras llegan a ser fractales de la naturaleza. Los fractales naturales o fractales artificiales en su mayoría vienen siendo únicos.

Cabe destacar que los fractales ya sean naturales o artificiales no están sujetos a alguna regla lo cual permite un número infinito de tipos de posibilidades a la hora de elaborar uno o en su defecto ya estar creando uno.

Una estructura que en los últimos años tomado gran posición entre las personas, ideal para realizar grandes artes, realizar tatuajes, fotografía y mucho más, los fractales son excelentes objetos geométricos.

Historia de los fractales

Todo comienza en el año 1854 con un matemático francés que quería estudiar las figuras geométricas llamado Henri. Asimismo, años más adelante comenzó a integrarse el arte de estudiar la geometría fractal como una verdadera ciencia.

A raíz de esto se hicieron estudios más enfocados y materializados a la búsqueda de una geometría exacta y maravillosa que ha sido impulsora de lo que llamamos la matemática moderna en toda la historia.

Hoy en día los fractales se convirtieron en un término más profundizado más que todo en el ámbito artístico y en la fotografía, siendo una geometría que muchas personas admiran por su estructuración y lo atractivo que puede lograr resultar ser a simple vista, el cual podemos encontrar de diferentes maneras.

Rellenando el espacio.

Es fácil extender a un fractal a 3d, muchos de los objetos que hemos visto antes. Por ejemplo, si vamos eliminando los tercios que bisecan cada cara de un cubo podemos generar un conjunto de Cantor tridimensional.

Los fractales en la naturaleza

Para ser precisos, los fractales se los encuentra en casi todos lados debido a que todo nuestro alrededor en realidad está rodeado por una geometría casi perfecta es, sino que no nos damos cuenta y se puede encontrar en copos de nieve, árboles e incluso hasta en movimiento de la niebla.

Tipos de fractales

No solo existen un solo tipo de fractales como mencionamos anteriormente, que se diferencian de diferentes maneras:

Lineales: Son los fractales del tipo más simple que existe en realidad, pues como su nombre lo indica todas sus líneas de componentes son lineales en diferentes sentidos.

Órbitas caóticas: este tipo de fractales se descubrió a partir de un estudio realizado por el matemático Edward Lorenz en 1.963, sobre órbitas caóticas, esto a pesar que caos y fractales no son sinónimos y tienen comportamientos distintos.

Autómatas celulares: este tipo de fractales los utilizaron por primera vez por los matemáticos John von Neumann y Stanislaw Ulam en 1948. Estos fractales se utilizan para representar cuerpos celulares.

Plasma: estos fractales se crean a partir de medidas al azar, lo cual los convierten en únicos e irreversibles. Esto se debe a que es un proceso aleatorio no reversible.

El conjunto fractal más famoso.

El más famoso de todos vendría siendo los fractales de mandelbrot, este el más estudiado, se conoce así en honor al Benoît Mandelbrot (1924-2010), que investigó sobre él en los años sesenta.

Se encuentra representados mediante algoritmo de tiempo de escape, los colores de los puntos pertenecen a un conjunto de la velocidad divergente correspondiente a los mencionados puntos.

Tatuajes de fractales y su significado.

Hoy en día los tatuajes fractales han sido los predominantes de la moda de los tatuajes, los diseños y combinaciones se han convertido en los predilectos por muchos, mejor ejemplo que el “lobo fractal” que seguramente te has topado con uno de ellos por internet.

Además, son un diseño moderno que encaja a la perfección en la piel, según el diseño que las personas deseen. Un estilo de artes adaptado a la perfeccion tanton en hombres como en mujeres, encajan en varios lugares del cuerpo.

Manta: Tatuaje de mantas, que pertenece a los fractales blanco y negro. Este tipo de fractales hará que la divinidad, la suerte y fortuna siempre estén a tu favor. Este fractal se suele confundir con un 30 pero este es totalmente diferente en su significado, quien lleve este va a tener suerte, divinidad y buena fortuna.

Átomo fractal: Aquí el átomo fractal, este tipo de fractales pertenece a los fractales animados el cual representa lo pequeño que puede llegar a ser algo, pero siendo muy importante a la vez.

Ejemplos de fractales.

Hay varias áreas donde se puede utilizar los fractales como ya se ha mencionado anteriormente como en paisajes fractales, matemáticas fractales, fractales en el arte, figuras fractales y fractales famosos, etc.

Mayormente la naturaleza proporciona muchos fractales, en cuestión de percepción, se encuentran dichos efectos geométricos que cumplan con todos los factores indicados para ser considerados como un Fractal.

Fractales matemáticas

Ecuación fractal

Intentos de definición rigurosa, la definición de fractal exitista en el año 2008 , lo cual género que no tuviera una definición matemática exacta ni de una aceptación.

Hay algunos intentos superficiales para dar una definición los cuales fueron realizados por:

Mandelbrot, definió en el año 1982 a un fractal como un conjunto cuya dimensión de Hausdorff-Besicovitch es estrictamente mayor que su dimensión topológica. El mismo dijo que su definición era incompleta

Este matemático dijo que tampoco era completa su definición la cual era:

Sullivan, que definió una de las categorías de fractales con su definición de conjunto cuasi autosimilar que hacía uso del concepto de cuasi-isometría.

Dimensión fractal.

Dicha ecuación fractal se puede definir como la diminuta cantidad de bolas de radio necesarias para recubrir el conjunto, como el límite.

O en función del recuento del número de cajas de una cuadrícula de anchura que intersecan al conjunto.

El método de Newton.

Este método de newton trata de encontrar por iteración las raíces de la función F (Z)-1 = 0.

Se itera la función F(Z) con cada uno de los puntos del plano complejo (x + iy), siendo Z=(x1 + iy1) hasta la convergencia de x1 i y1, según la fórmula a continuación:

Z_n+1 = Z_n – F(Z_n) / F’(Z_n), en donde F’(Z) es la derivada. Se ha sobrepasado con el algoritmo de la velocidad de convergencia, conceptualmente idéntico al de la velocidad de salida, y presenta igualdades con el método de Julia.

Los conjuntos de julia.

Los frutos de los trabajos de Pierre fatou y Gaston julia dejaron unos conjuntos en los años 1920, estos surgen como resultado de la aplicación reiterada de funciones holomorfas en busca de respuestas

Al analizar el caso específico de funciones polinómicas de grado mayor que uno deja como resultado que al aplicar consecutivas veces una función polinómica es muy posible que el resultado sea X

Al conjunto de valores de Z E C que no escapan al infinito se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de Julia.

Estos conjuntos se representan mediante un algoritmo de tiempo de escape, en que cada pixel se subraya según las veces de iteraciones necesarias para escapar.

Suele usarse un color especial, a menudo el negro, para representar los puntos que no han escapado tras un número grande y prefijado de iteraciones.

Familias de fractales:

El conjunto de Mandelbrot.

el conjunto de Julia es asociado a la reiteración de funciones de la forma que presenta conjuntos de una variedad sorprendente.

Dicha familia tendrá especial relevancia al quedar parametrizada en un mapa de fractales, popularizado en los años 1980, llamado conjunto de Mandelbrot.

Este conjunto M representa un mapa en que cada píxel, correspondiente a un valor del parámetro, se colorea de modo que refleje una propiedad básica del conjunto de Julia asociado.

En concreto, si el conjunto de Julia asociado a es conexo.

Iterando funciones de forma alternativa se generan los fractales oscilantes.

Características de un fractal.

Auto similitud.

Según B. Mandelbrot, un objeto es autosimilar si sus partes tienen la misma forma o estructura que el todo, aunque pueden presentarse a diferente escala y pueden estar ligeramente deformadas.

Los fractales pueden presentar tres tipos de auto similitud:

Auto similitud exacta. Este es el tipo más restrictivo de auto similitud: exige que el fractal parezca idéntico a diferentes escalas. A menudo la encontramos en fractales definidos por sistemas de funciones iteradas (IFS).

Cuasiautosimilitud: exige que el fractal parezca aproximadamente idéntico a diferentes escalas. Los fractales de este tipo abarcan duplicados menores y distorsionados de sí mismos.

Matemáticamente D. Sullivan concreto el criterio del cumulo cuasi auto-similar a partir del concepto de cuasi-isometría. Los fractales definidos por relaciones de recurrencia son normalmente de este tipo.

Autosimilitud estadística.

Es el tipo más débil de auto similitud: se exige que el fractal tenga medidas numéricas o estadísticas que se preserven con el cambio de escala. Los fractales aleatorios son ejemplos de fractales de este tipo.

Aplicaciones de los fractales.

Estos se pueden utilizar en todos lados como en: plantas fractales, en fractales en la música, fotos de fractales, fractales en la arquitectura, en cuadros fractales, fractales animales, etc.

Los fractales en las plantas.

¿Alguna vez te has fijado en los patrones de crecimiento que tienen las plantas?

Si las observamos más detenidamente, nos daremos cuenta de que se van repitiendo. Así, dos ramas de un árbol crecerán formando una ‘V’, y las ramitas que broten de ellas seguirán su ejemplo. A esto se le llama fractal en plantas.

A esto se le conoce como fractal. Y crean auténticas maravillas. ¿Quieres ver fractales en la naturaleza vegetal? Echa un vistazo a estas imágenes.

Fractales en la música.

El 21 de marzo de 1685 nació el clavecinista, organista y compositor alemán:

Johann Sebastian Bach. Sus obras son consideradas piezas artísticas debido a su profundidad intelectual, su perfección técnica y su belleza melódica.

Además, es reconocido como el último gran maestro del arte de contrapunto, técnica de composición musical que relaciona dos voces independientes para crear un equilibrio armónico

En dichas obras se pudo apreciar el equilibrio armónico gracias a que estaba formada por fractales

El alemán compuso sus piezas musicales pensando en Fuga y Canon, que son elementos musicales que usan la repetición de melodías en diferente escala o velocidad con o sin contrapunto, pero que no precisamente son la misma melodía.

El uso del canon y la fuga es similar a la naturaleza fractal, pero este término no se conocía en 1685 sino hasta 1975 cuando fue acuñado por el matemático Benoît Mandelbrot.

Además, en algunas obras clásicas de Beethoven, Bach y Mozart son ejemplos representativos según reveló un estudio.

El método que siguieron estos compositores, para integrar fractales y matemáticas era mediante una analogía entre una dimensión fractal y el número y la disposición de las diferentes notas de una obra o pieza.

Fotos de fractales.

La fotografía se puede definir como la captura de un momento para siempre, una foto puede capturar un fractal directa o indirectamente lo que permite apreciar dicho fractal.

Una de las obras más veneradas de los fractales, las fotográficas naturales de fractales pueden ser captadas desde una perspectiva exacta capaz de ser el adecuado para la toma de un autentico de fractal.

También podemos apreciar las imágenes mayormente en redes sociales más que todo, para las personas aficionadas a ella, además de poder realizar ilustraciones ejemplares a los patrones que los fractales.

Fractales en la arquitectura.

Benoit Mandelbrot acuñó el término Geometría Fractal en 1975 y él mismo observó su relación con arquitectura.

En esta disciplina se les encontró uso a los fractales, una vez si descubrió no ha parado de usarse por su eficacia e importante en esta

Se han llevado a cabo varios análisis y comparaciones con la arquitectura Fractal, porque se considera que muchos arquitectos de la antigüedad, basaron sus diseños en los principios fractales.

Importantes edificios de la antigüedad, arquitectura vernácula y el diseño urbano de ciudades alrededor de todo el mundo han presentado en su diseño patrones relacionados con estos. En losetas para piso son muy comunes los patrones de fractales.

Dentro de un sistema fractal debe haber una jerarquía hecho del cual la ciudad moderna carece. Una ciudad fractal y sin jerarquía es la famosa “La ciudad genérica” de Rem Koolhaas (conocido tanto por su obra como por sus escritos), una ciudad que carece de identidad conforme se expande y se aleja del centro.

Cuadros fractales.

Ya sabemos que las utilidades de estos son muy variadas, se pueden utilizar en casi todo, en este caso en cuadros fractales, los cuales son basados en hechos matemáticos los cuales rigen las formas de estos.

En los cuadros fractales se puede apreciar la calidad de los fractales blanco y negro, fractales dibujos, etc.

El fractal te permite hacer que tu obra sea lo más cercano a lo perfecto, por eso es que muchos artistas se rigen por las reglas que abarcan a estos.

Fractales animales

Cabe destacar que no podía faltar que los fractales se aprecian en los animales, debido a su grandeza y perfección. La naturaleza tiene formas caprichosas.

Algunas se pueden explicar gracias a las matemáticas mientras que en otras ha sido la evolución, o alguna explicación todavía por descubrir, la que rige las formas de animales, plantas y otros fenómenos.

Entre los patrones naturales que repasamos en esta galería hay simetrías, espirales, rayas o dunas.

Las matemáticas, la física o la química pueden explicar diferentes tipos de patrones de la naturaleza. En animales, esas formas y dibujos se deben a la evolución y a las necesidades reproductivas.

También conocida como diaethria anna, esta especie aparece en los bosques húmedos tropicales que se extienden desde México hasta costa rica. Las líneas negras de las alas

posteriores, sobre fondo blanco, crean un efecto similar a un 88 en las alas, que da nombre a la especie.

Sistemas dinámicos.

Pero, además, las formas fractales no sólo se presentan en las formas espaciales de los objetos, sino que se observan en la propia dinámica evolutiva de los sistemas complejos.

Dinámica que consta de ciclos (en los que, partiendo de una realidad establecida simple, acaban en la creación de una nueva realidad más compleja) que a su vez forman parte de ciclos más complejos los cuales forman parte del desarrollo de la dinámica de otro gran ciclo.

Las evoluciones dinámicas de todos estos ciclos presentan las similitudes propias de los sistemas caóticos.

Existe un libro llamado fractales de la naturaleza, es importante resaltar que este libro habla muy bien de lo que son los fractales que se encuentran en un espacio determinado.

Asimismo, también puede hablarse de que los fractales son impresionantes y que pueden encontrarse en realidad en casi cualquier sitio además de ser únicos y originales.

La forma de la nube, una montaña una costa o un árbol es incapaz de descubrir la forma sí, porque las nubes no son esféricas, ni las montañas cónicas ni las costas circulares, ni el tronco de un árbol cilíndrico, ni un rayo rectilíneo. Son formas geométricas con distorsiones.

A mi parecer la naturaleza es magnífica, es irregular y fragmentada, la naturaleza no solo presenta un grado mayor de complejidad, sino que esa se nos revela completamente.

La investigación de la morfología de lo “amorfo, deforme o extraño” representa un desafío a la existencia de estas formas

Para responder a este desafío decidí concebir y desarrollar una nueva geometría de la naturaleza para empezar a aplicarla a una serie de campos

Fractales y finanzas.

El padre de la geometría fractal es el matemático de origen polaco benoit mandelbrot, el cual escribió el libro fractales y finanzas.

En su libro el habla sobre las estructuras geométricas de diversos niveles de tamaño en los fractales.

Cada una se repite a pequeña escala, son ideales para reducir la rigurosidad hacia estas estructuras geométricas que están presentes en la cotidianidad. En nuestro ambiente, tan simples como una nube y complejas como una célula, tan visibles como los colores y además son súper fáciles de hallar.

Los Objetos fractales.

Lo que se puede apreciar en este libro sobre los objetos fractales es:

¿Qué son los objetos fractales? ¿Para qué sirven, cuál es su historia y por qué se llaman así?

Los fractales representan un método para entender una gran parte de la diversidad de fenómenos de la naturaleza y a la vez una teoría matemática.

Benoît Mandelbrot creó los fractales a principios de los años sesenta y hoy protagonizan investigaciones que se ocupan de física teórica, geografía, economía, biología, zoología, etc.

De modo que en la actualidad se puede decir que existe una concepción y una geometría fractales de la naturaleza.

Estas se basan, en esencia, en el concepto de autosimilitud, una propiedad exhibida por aquellos sistemas cuyas estructuras permanecen constantes al variar la escala de observación; en otras palabras:

Cuando las partes, por pequeñas que éstas sean, se parecen a todo.

Este libro es el primer ensayo dedicado a exponer la teoría. Lo que generó un gran avance matemático.

Es importante entonces que se puedan apreciar y estudiar estas figuras geométricas fantásticas, no importa que pase, debemos saber que nuestro mundo es impresionante en todos sus sentidos, no hace falta nada lo que hace falta es tener la curiosidad de estudiarlo.

En resumidas cuentas, los objetos fractales o fractales, son formas geométricas que, en diferentes perspectivas, siendo agrupadas, forman estructuras complejas y completas. Las formas fractales están presentes en todo el mundo y hasta el más despistado podrá percibirlas, ya sea en la calle o en los objetos fractales de la naturaleza.

Considerado de diferentes maneras, y con diferentes conceptos tanto para las matemáticas, como en la música, los fractales pueden verse involucrado en muchos aspectos, solo es cuestión de ser capaces de captarlos a simple viste.

¡Por cierto! Antes de que te vayas, queremos recomendarte esto que seguro que te interesa: